Du bienfondé des microfondations
 |
| De SanG froid... E |
Faisons tout de suite une mise au point : nombre de discussions mélangent allègrement le choix de partir d'une modélisation microéconomique avec la façon de modéliser ces comportements individuels. Expliquons-nous : les individus de cette économie ne sont pas vraiment votre tata Monique ou papy Raymond, mais des représentations mathématiques simplifiées. Le choix des représentations peut être plus ou moins judicieux : on peut par exemple supposer que tout le monde se comporte de façon rigoureusement identique, ce qui est, on le verra dans un post séparé, une hypothèse très forte. En attendant, on se concentre ici sur le concept même de modéliser les comportements individuels plutôt que les quantités agrégées directement, comme le font par exemple IS-LM ou OG-DG (voir chapitre 3.1 de Fluctuations et Crises).
Microcosmos
Alors pourquoi se casser la tête à partir des individus pour représenter l'économie? Après tout, dans les sciences naturelles, cette approche n'est pas forcément suivie: il n'y a qu'à voir la mécanique classique, qui analyse la chute des corps et le mouvement des astres sans se préoccuper des interactions entre les atomes qui les composent.La raison est notamment à trouver du côté des facultés d'adaptation de l'être humain : n'étant pas des rats de laboratoire, nos comportements, notamment grégaires, changent au cours du temps ou au gré des victoires (ou défaites) en coupe du monde. Les relations agrégées sont donc nécessairement de nature purement statistique, basées sur quelques dizaines ou au mieux centaines d'observations vu la faible fréquence des données macroéconomiques. On est très loin du big data, ce qui nous expose à des problèmes de validité statistique (on parlera dans un autre post des problèmes d'estimation dans le contexte des modèles DSGE). Et même avec de meilleures données, on n'est toujours pas à l'abri d'un changement de régime qui invaliderait le modèle pourtant plutôt représentatif jusque-là.
C'est l'essence de la critique de Lucas, qui postule de facto l'existence d'invariants dans nos comportements (individuels ou grégaires), qu'il convient donc d'isoler afin de rendre la modélisation aussi rigoureuse que possible. Prenons par exemple la courbe de Phillips
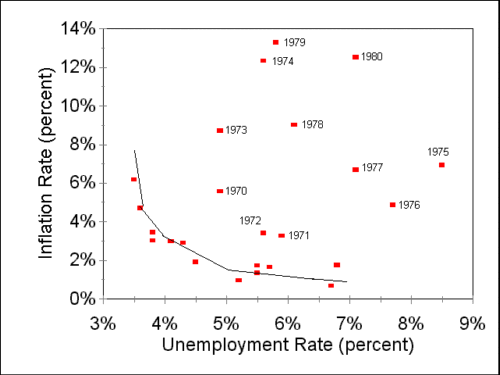, du nom de l'économiste britannique qui constata une forte régularité de la relation entre inflation et taux de chômage au Royaume-Uni entre 1860 et 1957. Pendant un temps, ceci avait aussi l'air de fonctionner pour les États-Unis : sur le graphique ci-contre, le taux d'inflation (en ordonnées) exprimé en fonction du taux de chômage (en abscisse) forme une jolie courbe bien régulière pour les années 50 et 60.Les pouvoirs publics ont alors tenté d'utiliser cette observation pour réduire le chômage, au prix d'un peu d'inflation. Malheureusement, l'inflation commença à s'emballer dans les années 70, au fur et à mesure que les gens se sont mis à ajuster leurs attentes d'inflation, ce qui eut pour effet de casser cette relation empirique. On voit ceci dans le graphique, dans lequel il est impossible de tracer une courbe du même genre à partir de 1970 (voir aussi chapitre 4.3.2 de Fluctuations et Crises).
D'un point de vue mathématique, cette relation, vue des années 50 et 60, dit juste que :
π = f(U)
Où π est l'inflation, U le chômage (de l'anglais unemployment) et f une fonction (on pourrait ici choisir la fonction inverse f(U) = 1/U vu la forme des données). Cette relation marche donc plutôt bien dans un premier temps, puis est invalidée par les données sans crier gare.
C'est ici qu'on voit le potentiel des microfondations : baser la modélisation macroéconomique sur celles-ci a pour but de la rendre plus robuste, en y injectant les résultats (souvent probants) de la microéconomie. Objectif ambitieux d'un point de vue mathématique mais pas dénué de sens. Dans le cas de la courbe de Phillips, la modélisation microfondée (qu'on épargnera au lecteur, voir ici pour plus de détails) donne un résultat bien différent, et injecte notamment les anticipations d'inflation, conformément à l'intuition de Phelps et Friedman (et à l'observation empirique des années 70):
πt = β Et πt+1 + γ yt
Où πt est l'inflation aujourd'hui, Et πt+1 est l'anticipation d'inflation pour la prochaine période, β l'escompte, yt l'écart de production et γ un coefficient.
Alors, une panacée les microfondations? Le lecteur avisé aura flairé l'arnaque dans l'équation ci-dessus : on ne parle plus de chômage ! Et il y a une raison (pas si bonne) à ça : on ne sait pas quelle microfondation utiliser pour construire la relation macro voulue entre inflation et chômage. C'est juste que c'est compliqué mathématiquement et qu'il faut faire de la recherche ! Et puis ces invariants sont-ils si invariants que ça ? On se souviendra notamment de ce post qui rapporte les différences de comportement face au partage selon le contexte culturel de l'expérience microéconomique. Ca n'est pas nécessairement insurmontable mais ça mérite encore plus de recherche...
Suspicion of Mass Destruction
Pour clore ce post, et pour dissiper des idées préconçues erronées, il convient de mentionner le théorème dit de Sonnenschein Mantel Debreu (SMD), du nom des trois économistes qui se sont penchés sur le sujet. Ce théorème est fréquemment invoqué comme démontrant la vacuité des théories économiques néolibérales. Sans rentrer dans des débats gauche-droite un peu vaseux, on peut résumer l'argument comme suit : les microfondations sont une construction absurde à laquelle on peut faire dire ce qu'on veut, d'où le sobriquet de SMD: Anything goes theorem. Dit autrement, faux implique n'importe quoi.Sauf que SMD ne dit pas vraiment ça... Voyons cela plus en détail : la fonction de demande nette agrégée, qui est la somme sur tous les marchés de la différence pondérée par son prix entre offre et demande pour le bien échangé sur le dit marché, caractérise complètement l'équilibre général. Dans ce cadre théorique assez précis, SMD nous apprend que la forme générale d'une fonction de demande nette agrégée n'est pas très contraignante. En particulier, il existe toutes sortes de fonctions respectant les propriétés génériques communes mais qui sont pathologiques au sens économique, car impliquant plusieurs (voire une infinité) d'équilibres possibles, des équilibres instables, etc. Ce que dit donc SMD, c'est que sans faire des hypothèses plus fortes sur notre économie que celles de base de la théorie de l'équilibre général, alors on ne peut pas écarter ces situations bizarroïdes de notre univers des possibles.
Mais cela n'invalide pourtant pas le principe de modélisation microfondée pour autant, car SMD ne dit pas que les microfondations vont systématiquement mener à un équilibre macroéconomique absurde. Et en pratique c'est même bien le contraire, car justement les choix particuliers amènent ce supplément de structure qui manque au cas général.
En conclusion, les microfondations sont un espèce de Graal de la modélisation, permettant d'apporter de la substance à des relations empiriques, l'économie ne bénéficiant pas de la même régularité observationnelle que les sciences naturelles. Elles sont cependant critiquées car malheureusement devenues l'Alpha et l'Omega de la macroéconomie, négligeant le fait que de trouver des microfondations solides est une gageure, et que cela se fait souvent au détriment du bon sens.
On se quitte sur l'énoncé du théorème, en essayant de rendre intelligible sa brutalité mathématique :
- Soit N le nombre de biens (et de prix) observés dans notre économie.
- Soit Pε l'ensemble des vecteurs de prix p qui peuvent exister (positifs et satisfaisant une condition mineure au bord) : c'est l'ensemble des configurations de prix que notre économie peut prendre
- Soit f une fonction de ces prix, qui doit posséder les caractéristiques suivantes :
- Etre continue (on peut la tracer sans lever le crayon)
- Etre homogène de degré zéro, c'est-à-dire que si on multiplie tous les prix par un même nombre, alors les valeurs que prend f sont inchangées (les fonctions constantes sont par exemple de degré zéro).
- Satisfaire à la loi de Walras, qui dit que p . f(p) = 0 (il s'agit d'un produit scalaire vu que l'on considere des vecteurs
- Alors il existe une économie d'échange telle que f soit la fonction d'excès de demande, associant à chaque prix l'excès de demande correspondant, pour chaque marché. L'homogénéité de degré zéro est logiquement attendue d'une fonction de demande, car on s'attend à ce qu'elle ne change que lorsque les prix relatifs changent. Quant à la loi de Walras, ceci n'est autre que la contrainte de budget dans une économie d'échange : la valeur des dotations initiales doit être égale à la valeur des attributions finales.
